Math is regarded as one of the most objective topics there is: there can only be one right answer to a question and your opinions about what it should or shouldn’t be are irrelevant. But, as we’re going to see, that may not always be the case.
The debate over the answer to zero divided by zero has polarized the STEM community and remains unsolved to this day. So, in this post, we are going to review the numerous opinions surrounding this seemingly straightforward question and provide some evidence for each of their claims. We are going to refute these claims not with the intention of picking a side on the debate, but to reveal the complexity of this topic that at surface level, seems quite elementary. And, if you read to the end, you’ll find our answer!
The three most common responses are based on the rules of division that contradict in this unique case. First, many argue that 0 / 0 = 0 because zero divided by anything is zero. On the other hand, there are those that say that 0 / 0 = 1, because any number divided by itself is one. Finally, others state 0 / 0 = undefined as any number divided by zero can’t be defined.
Now, let’s turn to the definition of division in order to gain a better understanding of the situation and potentially find some evidence for the proposed answers. When we are dividing a number (x) by another number (y), we are asking how many times does the number y “fit into” the number x. Or, more simply, y times “what” is equal to x. This means that the result of a quotient can be multiplied by the denominator in order to find the value of the initial number (the numerator). This seems to indicate that any number divided by zero is undefined unless the numerator is also zero, in which case the answer could be zero or any other number for that matter, because zero times multiplied by anything is zero. Showing that it can be any number doesn’t help us at all, so we have to find other means of answering this problem.
When dealing with situations such as this one in which you can’t simply plug it into the calculator to find the answer, we use the concept of limits. Limits are a topic in calculus in which we look at points on a function as they get infinitely close to a given number and then make an estimation about what the value of the point will be at that given number. So, to apply it to the problem at hand, we can use a function that will come out to 0/0 at some point and use limits to calculate the output at that point.
For example, if we plot the function sin(x)/x, we will get an output of 0/0 at x=0. We can see the function graphed below.
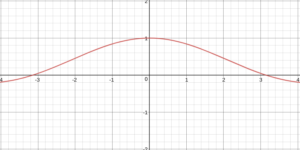
Now, we look at the limit of x as it approaches 0 and see that the function gets infinitely close to 1 at that point. So, this seems to indicate that the answer to zero divided by zero is one. But, don’t celebrate yet. If we manipulate the sine function, we see that we can, in fact, use this methodology and make it yield an infinite number of answers to our question. For example, if we use the function sin(2x)/x instead of sin(x)/x, we will still be at 0/0 when x=0, but the limit as x approaches zero is ½ instead of 1. This can be done for any number y or z in the function ysin(z*x)/x, yielding an infinite number of possible values for the limit as x approaches zero. Once again, this argument doesn’t prove anything and leaves us with the same unsatisfying answer: anything!
Not so simple after all, hugh?
After repeated attempts at solving this problem throughout history, the general final determination of zero divided by zero is, drum roll please, undetermined!
Now, this is definitely not the answer you were looking for or are satisfied with. But, that’s exactly the point: we wanted with this detailed examination of the age-old debate to demonstrate that math does have room for opinion and commentary and isn’t just an objective science with exclusive consensus. Many topics in math are yet to be determined and, who knows, maybe you could be the one to solve them?
Thank you for reading, we really hope you enjoyed this blog post! Please feel free to reach out to us at any time at [email protected] and we’d be happy to address any questions or concerns you have regarding this article.
