Around the world, math evolved in different ways across different cultures. Pi was discovered in Greece, but also in China. Our numbers are Arabic, and there is also an interesting case of tribal math in Ethiopia used in the 19th century that was reported by a European colonel.
The colonel was attempting to purchase cattle from a local tribesman. He wanted seven animals at the cost of 22 birr each. The tribesman not being numerate, the local priest was called to verify the total price.
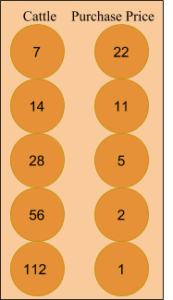
The priest then used a unique technique to calculate the price. He dug 2 parallel columns of holes. The right column was the purchase price and the left the cattle. Placing 22 stones in the right column and 7 in the left one to begin with, the priest then halved the purchase price while rounding down in each subsequent hole until reaching the number 1. Then he doubled the cattle number in the same number of holes.
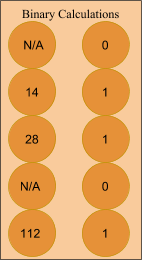 Then, the priest declared that even numbers were evil and he then removed the 22 and 2 from the right column. Along with the 22 and 2, he also removed the numbers that corresponded with them in the left column so the 7 and 56 were removed as well. Gathering the remaining piles in the left column- 14, 28, and 112 the priest put them all together and began to count the amount of stones in this ‘mega-pile’. They came out to 154 birr, which is 22 x 7.
Then, the priest declared that even numbers were evil and he then removed the 22 and 2 from the right column. Along with the 22 and 2, he also removed the numbers that corresponded with them in the left column so the 7 and 56 were removed as well. Gathering the remaining piles in the left column- 14, 28, and 112 the priest put them all together and began to count the amount of stones in this ‘mega-pile’. They came out to 154 birr, which is 22 x 7.
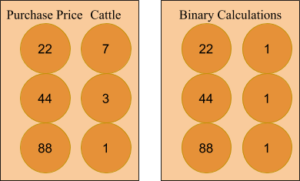
In fact, this method of multiplication will always work for multiplying whole numbers. That is because this seemingly simple ritual is actually a sophisticated physical implementation of binary multiplication. Here the right hand column where the number is halved repeatedly (rounding down) and the even numbers removed, becomes the binary equivalent of the number in base 10. Here 22 becomes represented as 10110 (read from bottom to top). Then the left hand column serves as a way of multiplying the powers of two for the designated volume number. By starting from the volume number of 7, and then doubling, each column becomes 7x that binary digit. 14 is (7 x 2), 28 is (7 x 4) and so on. Because 22 is 10110, 7 x 22 becomes [(0 x 1)+(7 x 2)+(7 x 4)+(0 x 8)+(7 x 16)] and adding that up gives the answer of 154. Is just as effective the other way around too. 7 in the right hand column and 22 in the left. Because there are no evil numbers, all that happens is that 22 is added to 44 and 88 or [(22 x 1)+(22 x 2)+(22 x 4)] which results as 154.

казино икс сегодня
казино х бонус при регистрации россия
Boy Girl Animal Baby Bathrobe Baby Hooded Bath Towel Infant Bathing Honey Baby
Pull-Ups Girls’ Cool & Learn Training Pants, 3T-4T, 66 Ct
вулкан слотс контакты
vulkanslots net